Geometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, which is what most people think of with the word "average", except that the numbers are multiplied and then the nth root (where n is the count of numbers in the set) of the resulting product is taken.
For instance, the geometric mean of two numbers, say 2 and 8, is just the square root of their product which equals 4; that is 2√2 × 8 = 4. As another example, the geometric mean of three numbers 1, ½, ¼ is the cube root of their product (1/8), which is 1/2; that is 3√1 × ½ × ¼ = ½ .
The geometric mean can also be understood in terms of geometry. The geometric mean of two numbers, a and b, is the length of one side of a square whose area is equal to the area of a rectangle with sides of lengths a and b. Similarly, the geometric mean of three numbers, a, b, and c, is the length of one side of a cube whose volume is the same as that of a cuboid with sides whose lengths are equal to the three given numbers.
The geometric mean only applies to positive numbers.[1] It is also often used for a set of numbers whose values are meant to be multiplied together or are exponential in nature, such as data on the growth of the human population or interest rates of a financial investment. The geometric mean is also one of the three classic Pythagorean means, together with the aforementioned arithmetic mean and the harmonic mean.
Contents |
Calculation
The geometric mean of a data set [a1, a2, ..., an] is given by
The geometric mean of a data set is less than or equal to the data set's arithmetic mean (the two means are equal if and only if all members of the data set are equal). This allows the definition of the arithmetic-geometric mean, a mixture of the two which always lies in between.
The geometric mean is also the arithmetic-harmonic mean in the sense that if two sequences (an) and (hn) are defined:
and
then an and hn will converge to the geometric mean of x and y.
This can be seen easily from the fact that the sequences do converge to a common limit (which can be shown by Bolzano-Weierstrass theorem) and the fact that geometric mean is preserved:
Replacing arithmetic and harmonic mean by a pair of generalized means of opposite, finite exponents yields the same result.
Relationship with arithmetic mean of logarithms
By using logarithmic identities to transform the formula, we can express the multiplications as a sum and the power as a multiplication.
This is sometimes called the log-average. It is simply computing the arithmetic mean of the logarithm transformed values of 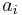 (i.e., the arithmetic mean on the log scale) and then using the exponentiation to return the computation to the original scale, i.e., it is the generalised f-mean with f(x) = log x.
(i.e., the arithmetic mean on the log scale) and then using the exponentiation to return the computation to the original scale, i.e., it is the generalised f-mean with f(x) = log x.
For normal frequency:
For frequency distribution:
Applications
Proportional growth
The geometric mean is more appropriate than the arithmetic mean for describing proportional growth, both exponential growth (constant proportional growth) and varying growth; in business this is known as the compound annual growth rate (CAGR). The geometric mean of growth over periods yields the equivalent constant growth rate that would yield the same final amount.
Suppose an orange tree yields 100 oranges one year and then 180, 210 and 300 the following years, so the growth is 80%, 16.7% and 42.9% for each year respectively.[Note: (210-180)/180=0.167 and 0.167*100=16.7]. Using the arithmetic mean calculates a (linear) average growth of 46.5% (80% + 16.7% + 42.9% divided by 3). However, if we start with 100 oranges and let it grow 46.5% each year, the result is 314 oranges, not 300, so the linear average over-states the year-on-year growth.
Instead, we can use the geometric mean. Growing with 80% corresponds to multiplying with 1.80, so we take the geometric mean of 1.80, 1.167 and 1.429, i.e. ![\sqrt[3]{1.80 \times 1.167 \times 1.429} = 1.443](/I/bdf37d001ecf15a3b4efa69a8c7d242b.png) , thus the "average" growth per year is 44.3%. If we start with 100 oranges and let the number grow with 44.3% each year, the result is 300 oranges.
, thus the "average" growth per year is 44.3%. If we start with 100 oranges and let the number grow with 44.3% each year, the result is 300 oranges.
Aspect ratios

The harmonic mean has been used in choosing a compromise aspect ratio in film and video: given two aspect ratios, the harmonic mean of them provides a compromise between them, distorting or cropping both in some sense equally. Concretely, two equal area rectangles (with the same center and parallel sides) of different aspect ratios intersect in a rectangle whose aspect ratio is the harmonic mean, and their hull (smallest rectangle which contains both of them) likewise has aspect ratio their harmonic mean.
In the the choice of 16:9 aspect ratio by the SMPTE, balancing 2.35 and 4:3, the harmonic mean is 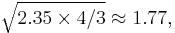 and thus
and thus 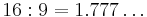 was chosen. This was discovered empirically by Dr. Kerns Powers, who cut out rectangles with equal areas and shaped them to match each of the popular aspect ratios. When overlapped with their center points aligned, he found that all of those aspect ratio rectangles fit within an outer rectangle with an aspect ratio of 1.77:1 and all of them also covered a smaller common inner rectangle with the same aspect ratio 1.77:1.[2] The value found by Powers is exactly the geometric mean of the extreme aspect ratios, 4:3 (1.33:1) and CinemaScope (2.35:1), which is coincidentally close to 16:9 (1.78:1). Note that the intermediate ratios have no effect on the result, only the two extreme ratios.
was chosen. This was discovered empirically by Dr. Kerns Powers, who cut out rectangles with equal areas and shaped them to match each of the popular aspect ratios. When overlapped with their center points aligned, he found that all of those aspect ratio rectangles fit within an outer rectangle with an aspect ratio of 1.77:1 and all of them also covered a smaller common inner rectangle with the same aspect ratio 1.77:1.[2] The value found by Powers is exactly the geometric mean of the extreme aspect ratios, 4:3 (1.33:1) and CinemaScope (2.35:1), which is coincidentally close to 16:9 (1.78:1). Note that the intermediate ratios have no effect on the result, only the two extreme ratios.
Applying the same geometric mean technique to 16:9 and 4:3 approximately yields the 14:9 (1.555...) aspect ratio, which is likewise used as a compromise between these ratios.[3] In this case 14:9 is exactly the arithmetic mean of 16:9 and 4:3 = 12:9, since 14 is the average of 16 and 12, while the precise harmonic mean is 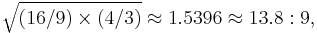 but these two means are approximately equal because both numbers are sufficiently close to 1.
but these two means are approximately equal because both numbers are sufficiently close to 1.
Spectral flatness
In signal processing, spectral flatness is described by the ratio of the geometric mean of the power spectrum to its arithmetic mean.
Notes and references
- ↑ The geometric mean only applies to positive numbers in order to avoid taking the root of a negative product, which would result in imaginary numbers, and also to satisfy certain properties about means, which is explained later in the article.
- ↑ 2.0 2.1 TECHNICAL BULLETIN: Understanding Aspect Ratios. The CinemaSource Press. 2001. http://www.cinemasource.com/articles/aspect_ratios.pdf#page=8. Retrieved 2009-10-24.
- ↑ US 5956091, "Method of showing 16:9 pictures on 4:3 displays", issued September 21, 1999
See also
- Arithmetic mean
- Arithmetic-geometric mean
- Average
- Generalized mean
- Geometric standard deviation
- Harmonic mean
- Heronian mean
- Hyperbolic coordinates
- Inequality of arithmetic and geometric means
- Log-normal distribution
- Muirhead's inequality
- Product
- Pythagorean means
- Quadratic mean
- Rate of return
- Weighted geometric mean
External links
- Calculation of the geometric mean of two numbers in comparison to the arithmetic solution
- Arithmetic and geometric means
- When to use the geometric mean
- Practical solutions for calculating geometric mean with different kinds of data
- Geometric Mean on MathWorld
- Geometric Meaning of the Geometric Mean
- Geometric Mean Calculator for larger data sets
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![\bigg(\prod_{i=1}^n a_i \bigg)^{1/n} = \sqrt[n]{a_1 a_2 \cdots a_n}.](/I/753061f377ecbca16901c207e944ecb9.png)
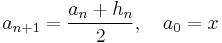
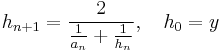
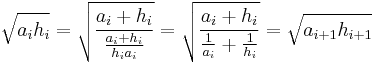
![\bigg(\prod_{i=1}^na_i \bigg)^{1/n} = \exp\left[\frac1n\sum_{i=1}^n\ln a_i\right]](/I/c53ae00033a50e8f0b68a7aac70662b9.png)
![GM = Antilog\left[\frac1n\sum\ logx\right]](/I/cdce6069596228c0eeaa5b27c3b758f2.png)
![GM = Antilog\left[\frac1n\sum\ f logx\right]](/I/df7032ab5da9abdc0e3b7472d4a3a36a.png)